Körpermaße Indizes

Body-Indizes zur Bewertung des Körpergewichts

Um zu ermitteln, ob ein Körperschema von der Norm abweicht oder auch ein Gesundheitsrisiko birgt wurden diverse Body-Indizes entwickelt. Ziel dieser Indizes ist es das Körpergewicht in Relation zur Statur zu setzen, da das Gewicht allein nicht aussagkräftig ist. Eine Person mit einer größeren Körpergröße z.B. kann auch bei einem höheren Gewicht nicht übergewichtig sein während eine kleinere Person bereits übergewichtig ist. Ein weiterer wesentlicher Einflussfaktor ist das Verhältnis von Muskelmasse und Fett. Hier spielt sowohl das Geschlecht als auch der Trainingszustand eine Rolle. Da Frauen allgemein eine geringere Muskelmasse haben ist das Geschlecht bei der Interpretation der Indizes zu beachten.

Was können die Body-Indizes?

Die Body-Indizes können einen Hinweis darauf geben, ob Über- oder Untergewicht bzw. ob ein Gesundheitsrisiko vorliegt. Des weiteren können sie Aussagen zum Trainingsstand machen. Immer ist zu beachten, dass die Indizes nur eine Indikation geben. Es handelt sich immer um eine starke Vereinfachung, die versucht aus leicht zu ermittelnden Daten auf die Fett- und Muskelanteile zu schließen.

Welche Body-Indizes gibt es?

Die Indizes verwenden unterschiedliche Eingangsgrößen um auf das Körperschema zu schließen. Die einfachsten verwenden nur Gewicht und Körpergröße. Dazu gehören der Ponderal Index, der Broca Index, Area Mass Index und der vielfach verwendete Body Mass Index BMI.

Eine wesentliche Erweiterung stellt der Body Shape Index (ABSI) dar, da er den Taillenumfang als wesentliche Größe in die Betrachtung mit einbezieht. Der Taillenumfang ist ein guter Indikator für die Fettverteilung im Körper. Das Gewicht selbst sagt ja nichts darüber aus, ob das Gewicht in Form von Muskeln oder in Form von Bauchfett oder Unterhautfett vorliegt.

Weitere Kennzahlen liefern das Verhältnis von Größe zu Taillenumfang (WHtR: Waist - Height Ratio) und das Verhältnis von Taille- zu Hüftumfang (WHR: Waist – hip ratio).

Ein für die Beurteilung des Trainingszustands wichtiger Index ist der FFMI. Der Fettfreie Masse Index (FFMI) ist ein Index wie das Gewicht zustande kommt ob durch Muskulatur oder durch Fett. Der FFMI ist hier aussagekräftiger, da er den Körperfettanteil mit berücksichtigt. Ein hoher FFMI signalisiert einen guten Trainingszustand also einen hohen Muskelanteil.

Rechner zur Berechnung der Body-Indizes

Auf dieser Seite sind Rechner zu den verbreiteten Indizes, die den jeweiligen Index berechnen und zur leichteren Interpretation teilweise auch grafisch darstellen. Da die Indizes unter Umständen recht unterschiedliche Ergebnisse liefern können mit dem Körperschemarechner alle Indizes parallel berechnet und verglichen werden. Der Körperschemarechner berechnet und bewertet die folgenden Körpermaßindizes: Body Mass Index (BMI), Broca Index, Ponderal Index, A Body Shape Index (BSI, ABSI), Taille-zu-Größe-Verhältnis (WHtR)), Taille-Hüft-Verhältnis (WHR).

Body Mass Index (BMI)

Der Body Mass Index (BMI) ist eine Maßzahl, die das Gewicht in das Verhältnis zum Quadrat der Körpergöße setzt. Der BMI ist ein grober Richtwert, da er weder Statur noch Gewichtsverteilung berüchsichtigt. Seit Anfang der 1980er Jahre wird der BMI auch von der Weltgesundheitsorganisation verwendet. Die jetzige BMI-Klassifikation der WHO besteht im Wesentlichen seit 1995.

Wie berechnet man den BMI?

Den BMI berechnet man indem man das Körpergewicht durch das Quadrat der Körpergröße teilt.

$BMI = \frac{m}{L^{2}}$

mit m : Körpergewicht in kg, L : Körperhöhe in m

Beispiel für die Berechnung des BMI

Ist zum Beispiel eine Person 1.75m groß und wiegt 65kg dann berechnet sich der BMI folgendermaßen:

$BMI = \frac{m}{L^{2}} = \frac{65}{{1.75}^{2}} = \frac{65}{1.75 \cdot 1.75} = \frac{65}{3.0625} = 21.2$

Mit dem BMI-Rechner kann der BMI einfach berechnet werden, indem man Größe und Gewicht eingibt.

Was sagt mir der BMI?

Die Interpretation des berechneten BMI Wertes erfolgt über den Vergleich mit den tabellierten Durchschnittswerten der Bevölkerung. D.h. der Normalbereich entspricht dem Durchschnitt in der Bevölkerung zur Zeit der Erhebung. Der BMI kann auch bei Kindern und Kleinkindern als Maß für die gesunde Entwicklung des Kindes verwendet werden. Der BMI wird nach derselben Formel wie der BMI von Erwachsenen errechnet jedoch altersabhängig interpretiert. Aus den BMI Tabellen kann abgelesen werden in welchem Bereich von starkem Untergewicht bis starkem Übergewicht der ermittelte BMI liegt. Die Tabellen unterscheiden sich für Männer und Frauen. Für Erwachsene gelten die Werte ab 19 Jahre und für Kinder und Jugendliche ist der entsprechende altersgerechte Wert zu nehmen.

Sei die Person aus dem Beispiel eine weibliche jugendliche im Alter von 16 Jahren dann entnimmt man der Tabelle für Frauen das ein BMI von 21.2 im Normalbereich liegt.

Alter

Starkes Untergewicht

Untergewicht

Normalgewicht

Übergewicht

Starkes Übergewicht

16 Jahre

BMI < 16.3

16.3 < BMI < 18.3

18.3 < BMI < 24.3

24.3 < BMI < 29.1

29.1 < BMI

BMI-Verlauf bei Kleinkindern

Die Diagramme zeigen den Verlauf der BMI-Bereiche für Kleinkinder im Alter bis 2 Jahren.

Jungen

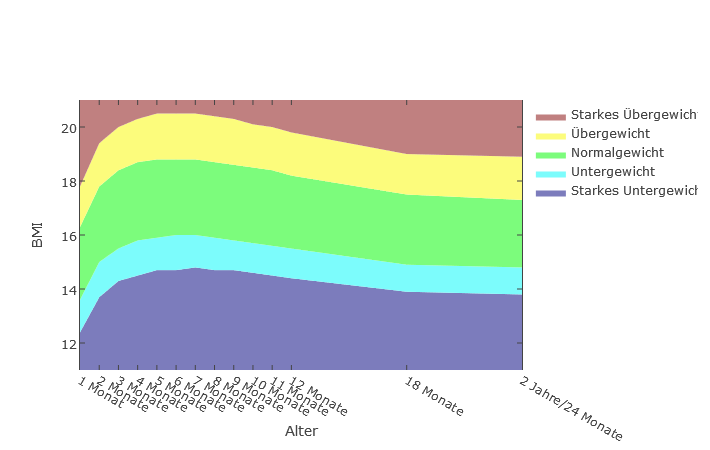
Mädchen

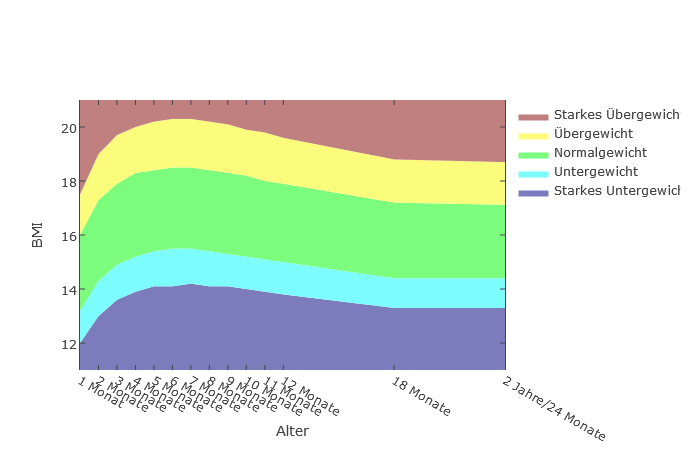
BMI-Verlauf bei Kindern und Jugendlichen

Die Diagramme zeigen den Verlauf der BMI-Bereiche für Kinder und Jugendliche im Alter von 2 bis 18 Jahren.

Jungen

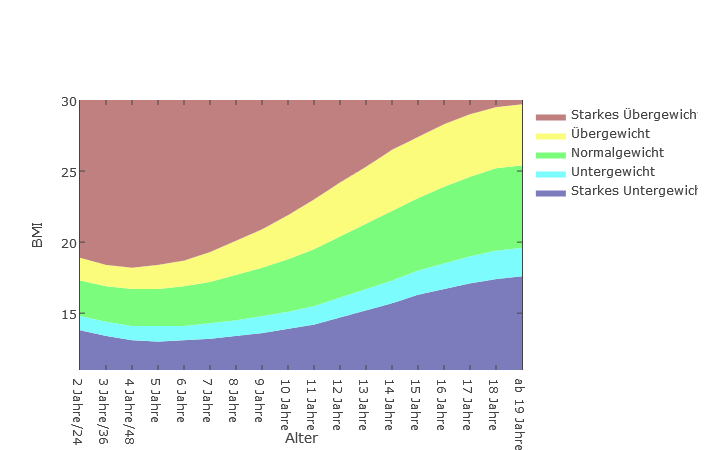
Mädchen

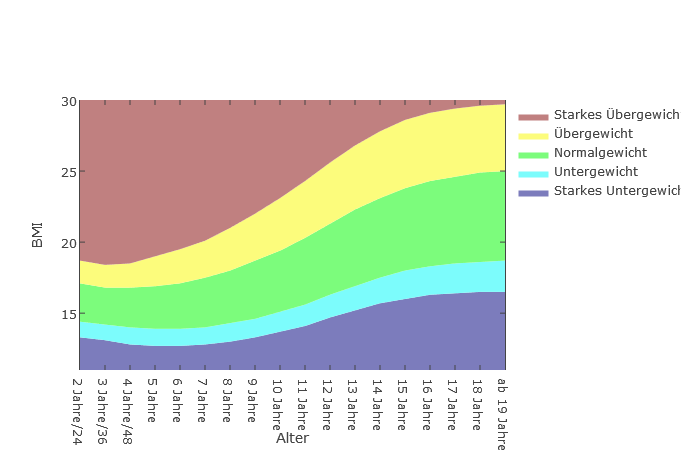
BMI-Verlauf im Gewicht zu Größe Diagramm

Aufgrund des unterschiedlichen Wachstums bei Kindern ist die Relation von Größe zu Gewicht unter Umständen sinnvoller. Aber auch ganz allgemein ist es interessant den BMI in Bezug auf die Größe zu betrachten. Die Frage welchen BMI bei welcher Größe beantwortet das BMI Gewicht über Größe Diagramm. Das Diagramm zeigt den Verlauf der BMI-Bereiche in Bezug auf Körpergröße zu Körpergewicht. Der BMI-Rechner gibt in der grafischen Einordnung des Ergebnisses auch die Gewichtsgrenzen bei der angegebenen Größe mit an.

Jungen 50 - 100cm

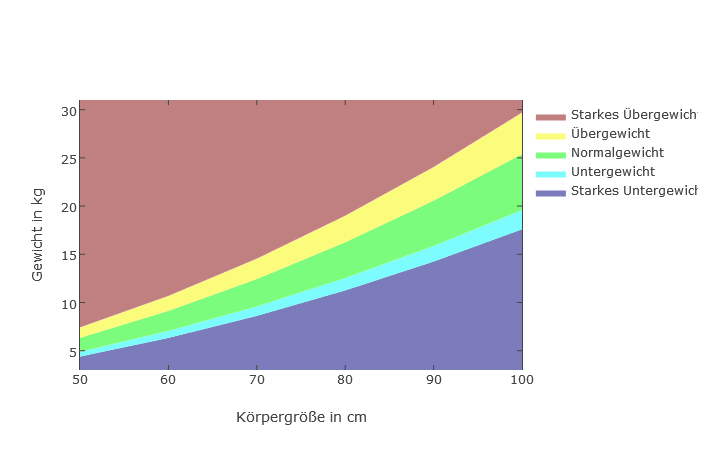
BMI_Groesse_Gewicht_Diagramm_50-100_Jungen

Mädchen 50 - 100cm

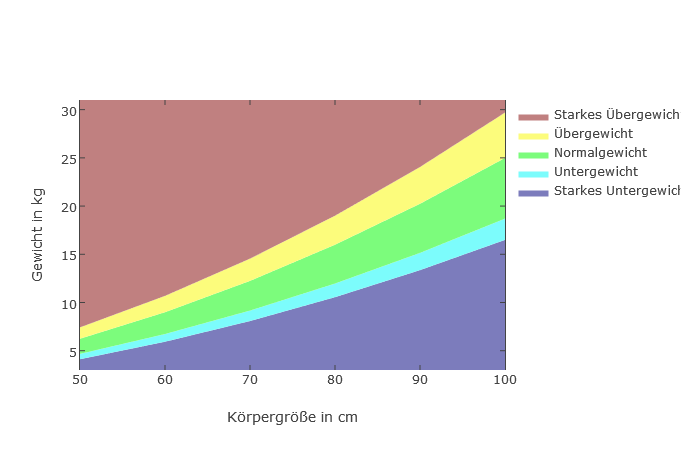
BMI_Groesse_Gewicht_Diagramm_50-100_Maedchen

Jungen 100 - 150cm

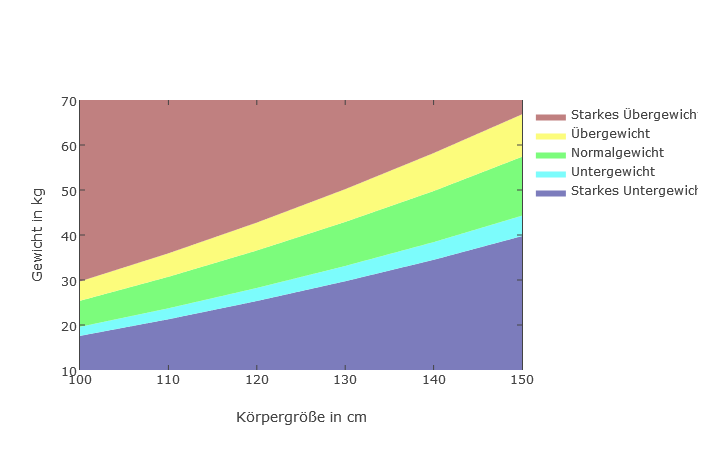
BMI_Groesse_Gewicht_Diagramm_100-150_Jungen

Mädchen 100 - 150cm

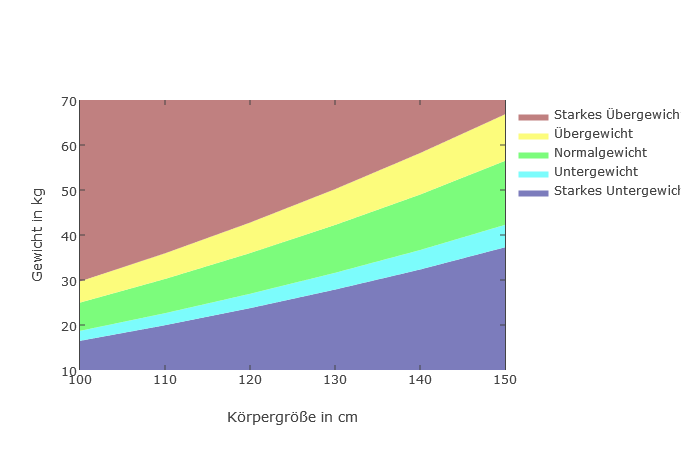
BMI_Groesse_Gewicht_Diagramm_100-150_Maedchen

Ponderal Index (PI)

Der Ponderal-Index ist eine Maßzahl zur Beurteilung des Körpergewichts im Verhältnis zur Körpergröße, ähnlich dem Body-Mass-Index. Im Unterschied zu diesem wird das Gewicht jedoch durch die dritte Potenz der Körpergröße geteilt also auf ein Volumen bezogen. Ponderal Index Werte zwischen 11 und 14 kg/m3 gelten als normal.

Ponderal-Rechner

Wie berechnet man den Ponderal Index?

$PI = \frac{m}{L^{3}}$

mit m : Körpergewicht in kg, L : Körperhöhe in m

Beispiel für die Berechnung des Ponderal Index

Ist zum Beispiel eine Person 1.75m groß und wiegt 65kg dann berechnet sich der Ponderal Index folgendermaßen:

$PI = \frac{m}{L^{3}} = \frac{65}{{1.75}^{3}} = \frac{65}{1.75 \cdot 1.75 \cdot 1.75} = \frac{65}{5.36} = 12.1$

Damit liegt der Wert in dem Beispiel im Normalbereich.

Broca Index (BI)

Der Broca-Index ist ein Maß zur Berechnung des Normalgewichtes einer Person. Er wurde von Paul Broca, einem französischen Arzt, Chirurgen und Anthropologen (1824–1880), entwickelt. Die Broca-Formel für das Idealgewicht von Frauen lautet: Körpergröße in Zentimetern minus 100 und von dem Ergebnis 15 Prozent abziehen. Die Broca-Formel für das Idealgewicht von Männern lautet: Körpergröße in Zentimetern minus 100 und von dem Ergebnis 10 Prozent abziehen. Der Broca-Index erlaubt lediglich eine grobe Einschätzung und trifft für den Bereich mittlerer Körpergrößen am besten zu.

Broca-Rechner

Wie berechnet man den Broca Index?

Die Broca-Formel für das Normalgewicht lautet: Körpergröße in Zentimetern minus 100 ergibt das Normalgewicht in kg.

$BI = L - 100$

mit L : Körperhöhe in cm

Beispiel für die Berechnung des Broca Index

Ist zum Beispiel eine Person 1.75m groß dann berechnet sich das Normalgewicht folgendermaßen:

$BI = L - 100 = 175 - 100 = 75$

D.h. das Normalgewicht beträgt 75kg. Für das Idealgewicht müssen bei einem Mann 10% also 7,5kg abgezogen werden. Damit ist das Idealgewicht wenn es sich bei dem Beispiel um einen Mann handelt 67,5kg. Für eine Frau müssen 15% entsprechend 11,25kg abgezogen werden. Damit ist das Idealgewicht für eine Frau dann 63,75kg.

Vergleich von BMI, Ponderal Index und Broca Index

BMI-Verlauf im Gewicht zu Größe Diagramm

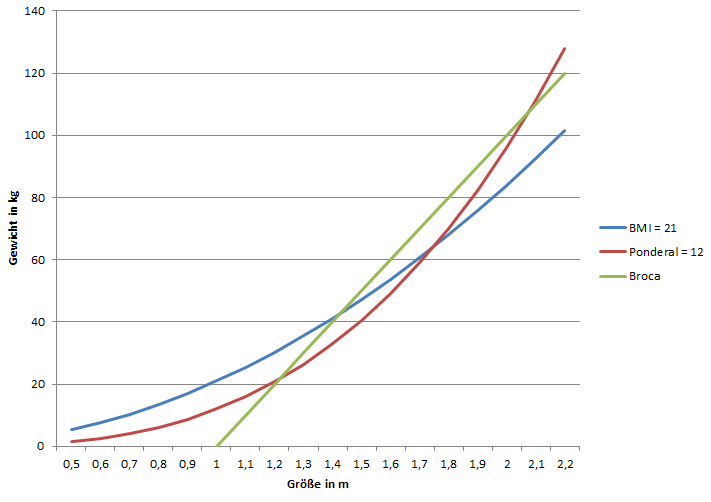
Das Diagramm zeigt Beispielhaft den Verlauf von BMI, Ponderal und Broca Index in der Relation von Größe zu Gewicht. Für Durchnittsgrößen im Bereich 1,70m bis 1,80m liegen die Indizes dicht beieinander. Der Unterschied zwischen Volumen und Fläche ergibt für große und kleine Personen jedoch einen signifikanten Unterschied.

Body Shape Index (BSI oder ABSI) Rechner

ABSI-Rechner

Der Body Shape Index (ABSI) sagt etwas über die Körperschemaverteilung. Je höher der ABSI ist, desto höher ist der Anteil an Bauchfett gegenüber sonstigen Körperanteilen wie Muskulatur oder Unterhautfett an Armen, Beinen oder OberKörper.

$ABSI = \frac{U}{{BMI}^{\frac{2}{3}} \cdot \sqrt{L}}$

mit U : Taillenumfang in m, L : Körperhöhe in m und dem BMI : Body Mass Index

Der Risikoindex ABSIz errechnet sich mittels der empirisch ermittelten Tabellenwerte für den ABSI für Männer und Frauen.

$ABSIz = \frac{ABSI - {ABSI}_{mean} (Alter)}{{ABSI}_{std} (Alter)}$

mit den Indizes mean : Mittelwert und std : Standardabweichung

ABSI Tabellen

ABSI Tabelle Frauen ABSI Tabelle Männer

Area Mass Index (AMI) Rechner

AMI-Rechner

Der Area Mass Index (AMI) ist eine Kenngröße aus der Anthropometrie und stellt das Verhältnis der Körpermasse eines Menschen – gemessen in Kilogramm (kg) – zu seiner tatsächlichen Körperoberfläche – gemessen in m² – dar, wobei die Körperoberfläche wiederum vom individuellen Körperbau (Statur) und dem Geschlecht einer Person abhängt. Die Körperoberfläche eines Menschen ist gleichzeitig die Fläche seines Wärmeaustauschs mit der Umgebung. Die Wärmeerzeugung des Menschen, die zur Aufrechterhaltung der Körpertemperatur notwendig ist, hängt von der Masse - genauer gesagt - von der Muskelmasse ab. Das Verhältnis von Körpermasse zur Körperoberfläche ist nicht konstant, sondern wird durch die Körperform bestimmt. Gedrungene Körper haben immer eine erheblich kleinere Körperoberfläche pro kg Körpermasse als schlanke Körperformen. Insofern geben schlanke Körperformen erheblich mehr Energie in Form von Wärme an die Umgebung ab als gedrungene, sofern die Bedingungen des Wärmeaustauschs (Temperatur der Umgebung, Isolation durch Kleidung etc.) identisch sind.

AMI für Frauen:

$AMI = 0.865 \frac{m}{L^{2}} + 18.65$

AMI für Männer:

$AMI = 1.048 \frac{m}{L^{2}} + 16.08$

mit m : Körpergewicht in kg, L : Körperhöhe in m

Waist-to-Height Ratio (WHtR) Rechner

WHtR-Rechner

WHtR (Waist-to-Height Ratio ‚Taille-zu-Größe-Verhältnis‘) bezeichnet das Verhältnis zwischen Taillenumfang und Körpergröße. Es soll eine Aussage über die Verteilung des Körperfetts machen und somit eine größere Aussagekraft bezüglich der gesundheitlichen Relevanz von Übergewicht erlauben. Für Unter-40-Jährige ist ein Wert über 0,5 kritisch. Im Alter von 40 bis 50 liegt die Grenze zwischen 0,5 und 0,6, bei über Fünfzigjährigen bei 0,6.

$WHtR = \frac{U}{L}$

mit U : Taillenumfang , L : Körperhöhe

Waist-to-Hip Ratio (WHR) Rechner

WHR-Rechner

Als Taille-Hüft-Verhältnis (Waist-hip ratio oder Waist-to-hip ratio (WHR)) wird das Verhältnis zwischen Taillen- und Hüftumfang angegeben. In der Sportmedizin wird der Quotient aus Bauchumfang und Hüftumfang auch als HBU bezeichnet. Der Bauchumfang wird in der Mitte zwischen Beckenkamm und Rippenbogen parallel zum Boden gemessen. Der Hüftumfang ist das größte Maß über dem Gesäß. Die DGSP gibt in der Leitlinie Vorsorgeuntersuchung im Sport folgende Werte für den HBU an: Frauen: Normalgewicht < 0,8; Übergewicht 0,8–0,84; Adipositas > 0,85. Männer: Normalgewicht < 0,9; Übergewicht 0,9–0,99; Adipositas > 1,0

$WHR = \frac{U}{H}$

mit U : Taillenumfang , H : Hüftumfang

Körperfettanteil Rechner

Körperfett-Rechner

Der Rechner berechnet den Körperfettanteil mittels der Navy Methode und der YMCA Methode. Die Methoden berechnen einen groben Schätzwert für den Körperfettanteil.

$KFA(Navy, Frauen) = 163.205 \cdot \log (Taille + Hüfte - Hals) - 97.684 \cdot log(L) - 104.912$

$KFA(YMCA, Frauen) = \frac{74.11 \cdot Hüfte - 3482}{m} - 8.2$

$KFA(Navy, Männer) = 86.010 \cdot \log (Taille - Hals) - 70.041 \cdot log(L) + 30.30$

$KFA(YMCA, Männer) = \frac{74.11 \cdot Hüfte - 4464}{m} - 8.2$

mit Taille : Taillenumfang in cm, Hüfte : Hüftumfang in cm, Hals : Halsumfang in cm, L : Körperhöhe in cm , m : Gewicht in kg

Formeln zur Berechnung des FFM und FFMI

$FFM = Gewicht \cdot \frac{100 - Körperfettanteil}{100}$

$FFMI = \frac{FFM}{{Grösse}^{2}} + 6.3 \cdot (1.8 - Grösse)$

Einheiten sind Körperfettanteil in Prozent, Grösse in m und Gewicht in kg

Bewertung des Körperschemas

Körperschemarechner

Der Körperschemarechner berechnet und bewertet die folgenden Körpermaßindizes:

Body Mass Index (BMI)
Broca Index
Ponderal Index
A Body Shape Index (BSI, ABSI)
Taille-zu-Größe-Verhältnis (WHtR))
Taille-Hüft-Verhältnis (WHR)

Grundumsatz, Leistungsumsatz und Sportumsatz Rechner

Kalorienumsatzrechner

Der gesamte Energieumsatz besteht aus mehereren Komponenten. Der Grundumsatz beschreibt den Energieaufwand um Körpertemperatur und grundlegende Körperfunktionen aufrecht zu erhalten. Dazu kommt der Leistungsumsatz der den Aufwand für Aktivitäten wiederspiegelt und der Sportumsatz.

Reduzierte Masse bei einem BMI ab 30 kg/m²

$m_{r} = \frac{3 (L - 100) + m}{4}$

mit m_r : reduziertes Körpergewicht in kg, m : Körpergewicht in kg, L : Körperhöhe in cm

Grundumsatz GU

$GU = 10 m + 6.35 L - 5 a + s$

mit GU : Grundumsatz in kcal, m : Körpergewicht in kg, L : Körperhöhe in cm, a : Alter in Jahren, s spezifischer Geschlechtswert s= 5 Mann und s= -161 Frau

Leistungsumsatz LU

$LU = (\frac{\sum {PAL}_{i} \cdot h_{i}}{\sum h_{i}} - 1) GU$